ルベーグ積分 ~穴だらけでも面積が知りたい~
積分は関数グラフの面積を求める方法ですけど、きちんと積分が求められるためには、関数グラフが連続で滑らかでなければなりませんよね。↓こういう、途中穴があいたような関数には不適ということです。

面積を求めるのですから、こんなものがうまく求められないのは、当然といえば当然です。でも、不便に感じることがあります。上の関数でどうしても面積を出したければ、穴の開いている前後に範囲を分けて、それぞれで積分して足すことになります。面倒ですね。
あと、↓こんな関数になると、もはや色々手が付けられなくなります。
ディリクレの関数
x=2/3とかなら1だけど、x=√2とかなら0になるということです。不連続すぎてグラフにかくことすら出来なくなりますね。

むりやりかくと、こんなイメージにでもなるでしょう。スッカスカですね。0と1をいったりきたりしているわけですが、不連続すぎてその様子が目に見えません。
これの積分を求めたいとしたらどうしましょう?
最初の例は穴があいていただけなので、それを分けて領域を分ければ済んでいましたが、今度は穴しかあいてないので、領域を分けるなんて不可能です。それでもこいつの面積が知りたいのです。これは極端な例かもしれませんが、積分はあらゆる分野の基本演算であり、穴だらけの関数を積分しなければならない機会は意外と多くあるので、こういうのに柔軟に対応できないのは、結構困ります。
そこで使われるのが、ルベーグ積分です。これに対して普通の積分はリーマン積分といいます。リーマン積分は極限が絡むと面倒になりがちでしたが、ルベーグ積分は極限が絡んでも何食わぬ顔で積分できてしまうのがウリです。また、ルベーグ積分できてリーマン積分できない関数はありますが、リーマン積分できてルベーグ積分できない関数はないので、完全上位互換ということになります。
ということでルベーグ積分を使うのは非常に有意義なのですが、扱うための下準備が多すぎて中々手が出しにくいモノであることも事実です。そこで本記事ではごく単純に、ルベーグ積分のこころを記していきたいと思います。イメージは大事よ。
ルベーグ積分のこころ
リーマン積分(普通の積分)はどうやってして面積を求めていたかというと、↓このように横方向の領域を短冊状に分割し、それぞれの長方形の面積を求めて足し合わせるということをやっていましたね。

しかしこの方法は滑らかな関数だからこそできることであり、途中地面に穴があいていると、この領域分けがうまくできなくなるのです。地面を基準にして横方向に分割したからなんですよね。地面に穴があいているかどうかの吟味をしていなかったわけです。
ルベーグ積分は領域をまず縦方向に分割します。そして、その領域にグラフがきているときの地面がどこかを調べます。

↑こんなイメージです。リーマン積分とは逆に、幅のことは後から考えるんですね。こうすれば、地面に穴があいているかどうか予め見極めたうえで、それぞれの領域に対して考えることができます。

地面の領域が定まったら、後はリーマン積分と同じように横×縦でそれぞれの長方形の面積を求めることになるのですが、単純に求められない場合があります。
縦方向に領域を分割したので、縦の長さは決まりきった簡単な値になりますけど、横の長さが不連続だったり穴があいていたりする可能性があるわけです。もともとそれで困っていたので、当然ですね。そもそも↑あのグラフは単調増加ですが、↓こんなふうに領域が分かれてしまう場合もあります。

↑縦の領域①②③に分け、それに対応する地面を下側の①②③として表記しています。①とか②は飛び地になりますよね。この場合も同様、横×縦のようにして面積を求めようとしていたので、果たしてこの飛び地の領域を横の長さと呼んでいいものか疑問があります。
そこで、この横の長さを一般化して扱いやすくしてしまいます。どんなに不連続だったり穴があいていたり、飛び地になって分断されていたりしても、これを一つの領域(集合)として扱って、「その領域に対する長さ」をむりやり決めてしまうわけです。この一般化された「長さ」のことを測度といいます。途中穴があいていようと、いやいやそれは、「長さ」ですと言い切るのです。
「長さ」に対応して新しく定義した「測度」を横の長さとして、横×縦で面積を求めて足し合わせる、これがルベーグ積分のこころです。なんとなく気持ちはわかるでしょうか。これならたとえグラフが穴だらけでも、「測度」さえちゃんと求められたら、横×縦で面積が出せそうですよね。
測度のこころ
長さに対応して新しく定義した測度。領域(集合)に対して、何らかの値を返す関数です。これを一般化した新しい「長さ」と呼ぶわけです。
そんな適当なこと言っていいのかと思われそうですけれど、いいんですよ。実はこの議論をしている間は、まだ面積すら定義されていないわけです。面積は積分から定義しますからね。その積分をいま定義しようとしているので、面積もまだないのです。きちんと整合性がとれていれば、自由に決めちゃっていいのです。*1
領域(集合)に対する測度は、
というような関数で表します。返ってくる値は0以上の実数で、そのまんま、領域に対する「長さ」を表します。

数直線上の連続した領域であれば、測度は数直線上の長さとして返します。「終端-始端」で得られますね。領域に穴があいている場合は、二つに分けて足すことができます(完全加法性といいます)。
また、測度の関数は集合が入力なので、上の例で「空集合」を入れてみたように、「実数全体の集合」とか「有理数全体の集合」とかも入れられます。実数全体の測度は∞、有理数全体の測度は0になります。どっちも無限集合だけど、実数の方が有理数よりも詰まってる(濃度が大きい)からこの違いが生じる*2のですけど、ここまできて恐縮ですが、濃度の話は割愛します。
勝手なイメージ:有理数は離散な点が無限にあるだけ→点一つ一つの測度は0→0を無限に足しても0。実数はすべて繋がっており、連続な領域→数直線の0~1の長さを1と定義したのだから、その比でどこまでも大きくなる。
有理数の集合に対する測度
ということですね。無理数の場合どうなるかというと、無理数は「実数-有理数」ですから、∞-0=∞になります。実数の測度と同じになります。無理数の方が詰まってるんですよね。今回これだけ抑えていただければOKです。
ルベーグ積分してみる
準備は整ったので、実際にルベーグ積分してみましょう。まずは普通の関数から。
∫[0→1] 2x dx
リーマン積分で普通に求めると、こうなりますね。
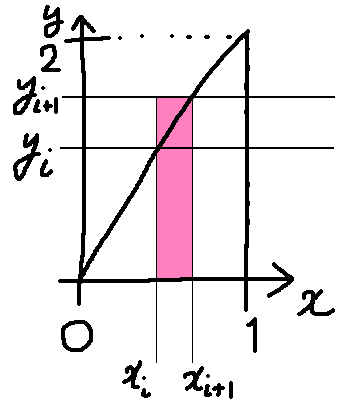
まず、縦方向に個の領域に分割します。
となるようにして、
となる領域を考えます。
ルベーグ積分ではまず、この縦方向に分割した領域の地面を調べるのでした。各領域に対する地面の範囲を求めます。
これは簡単ですね。ですから、
になります。
ここで、縦方向は等間隔に分割したとして、であるとします。すると、地面の範囲は
になります。
この領域に対する測度を求めます。ということですね。これは数直線上の領域なので、「終端-始端」で簡単に値が求まります。
これで横の長さに対応する測度が求まりました。縦の長さと掛ければ、番目の領域の面積が求まります。
縦の長さはでも、
でも、どっちでもいいです。リーマン積分のとき、縦の長さとして始端側と終端側、どっちを選んでも、収束すれば同じになる、というのと同じです。ここでは簡単のため、
とします。面積は
になりますね。
ですから、
が面積になります。
あとは全部の領域の面積を足し合わせればいいですね。
領域の数を無限大にしてやれば、
おお、きちんと1になりますね。こんな感じです。
∫[0→1] ディレクレの関数(x) dx
ディリクレの関数を0から1で積分します。当然リーマン積分は不可能ですけど、ルベーグ積分は可能です。やってみましょう。
ディリクレの関数

これの面積が求められたら感動モノです。
やることは同じで、まずは縦方向に領域を分割します。値域が0か1なので、0付近、1付近、その間、の3つを考えます。

まず、0付近の領域です。これに対応する地面は、「0から1の範囲にある無理数全体」ですよね。これの測度を求めます。先の議論で無理数全体の測度は∞で、0から1の範囲とすれば
と同じになります。したがって、測度は
になります。縦の長さは
ですので、面積は
になります。
より、面積は
ですね。
次に間の領域です。ディリクレの関数がこの間の値をとることはないので、地面はありません。空集合
になります。
ですから、測度は0になります。面積も0ですね。
最後は1付近の領域です。これに対応する地面は、「0から1の範囲にある有理数全体」ですよね。有理数の測度は0でしたから、これの測度は0です。なので面積も0になります。
以上から、全部の領域の面積を足し合わせるとになります。これを
とすると
になりますから、なんと積分結果は0になります。
こうしてルベーグ積分できました。こいつの面積は0だったのですね……スカスカの有理数のときしか立ち上がらないグラフなので、0が無限に足し算されていたようなイメージです。なんということでしょう……ちなみに逆に有理数のとき0、無理数のとき1になるようにした関数でやってみると、積分結果はちゃんと1になります。
ルベーグ積分のこころはこんな感じです。何だか、めんどくさい部分を新しい概念「測度」に全部押し込んだような感じになっていますけど……だからルベーグ積分をやると初めに測度が出てきて、測度について詳しく学ぶことになるんですね。