n乗根の筆算
過去ブログの転載です。
2乗根(ルート)の筆算
ルートの筆算は一部の界隈では有名です。次のように行いますね。
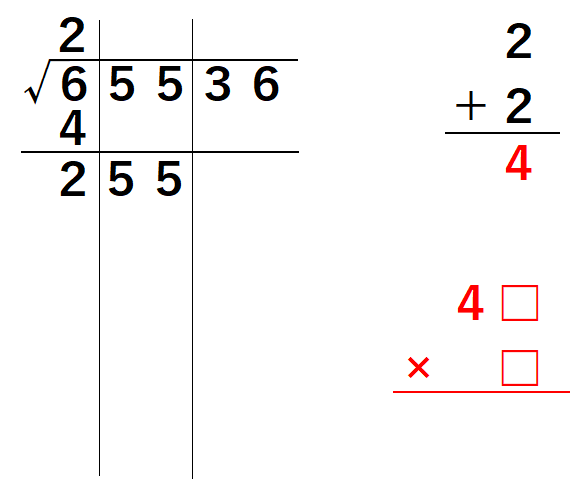
2桁をひとかたまりにして計算しますね。小数点の位置を境にする感じで区切ります。
この場合は最初の数字が6ですから、2乗して6を超えない最大の整数として2を入れます()。よって、百の位は2になります。6-4=2として、次の2桁を下ろします。
同時に、一方でもう一つの筆算を用意します。百の位が2だったので、2+2=4を計算し、さらに4□×□を計算します(□には同じ数字が入ります)。この計算結果が255を超えない最大の数となるように□を決めるわけです。ここが難しいのですが、これを当てられるようになれば、ルートの筆算は手にしたようなものです。

この場合は□に5を入れると45×5=225となって、255を超えない最大の数になりますね。□に入れた5が、まさに十の位の答えとなります。255-225=30で、次の36を下ろします。
後は同様です。もう一つの筆算で45+5=50を計算し、50□×□が3036を超えない最大の数となるように□を決めます。

□は6になります。506×6=3036となって、3036-3036=0。ここで0が出て来たので、計算終了です。答えは256になりますね。
などは1.4142…と無限に続いてしまうので、最後の0は永久に現れません。
3乗根はどう計算するか
3乗根に限っては特殊な方法で計算できるそうですが、上記の方法を拡張することにより、3乗根や4乗根、果てはn乗根を計算することが出来ます。
上記の方法の拡張で、3乗根を計算してみましょう。
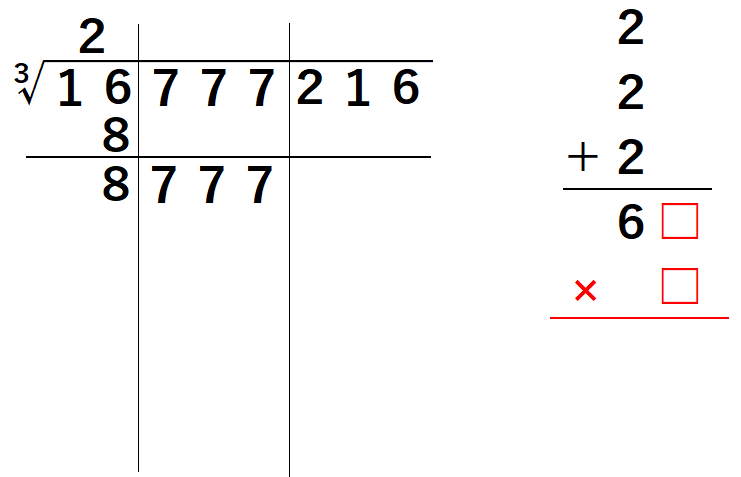
3乗根の場合は3桁区切りにします。最初の桁は、3乗して16を超えない最大の整数になります。なので、百の位は2になります。16-8=8を下ろし、777を下ろします。ここまではルートの筆算とだいたい同じですよね。
次からが大変です。2つ目の筆算では、2を3回足します。次に6□×□の筆算を作りますが、ここではまだ終わりません。

このように、今度は3つ目の筆算を作る必要があります。今度はを3回足して12にして、その後ろに0を2つ付け、1200にします。それに6□×□の答えを足し、更に□を掛けます。3乗根なので、□が3回登場するんですね。この最後の計算結果が、8777を超えない最大の数になるように□を決め、それが十の位の答えになるのです。難しいでしょ。

□に5を入れると、最大の数である7625になります。よって十の位は5です。8777-7625=1152と、216を下ろします。
次の桁を求めるたびに、右の筆算はそれぞれ書き直さなければなりません。

次の筆算はこうなるわけですね……25を3回足した筆算と、を3回足した筆算を用意して、同じ計算をして□を求めます。

□には6が入るので、答えは256となります。
4乗根の筆算
4乗根の筆算の場合、4桁に区切って筆算が右に3個出てきます。後は似たような要領です。

こんな感じになります。2を4回足したもの、を6回足したものの後ろに0を2個、
を4回足したものの後ろに0を3個、として、後は同様にして□を求めるという流れです。これら足す回数が4回、6回、4回、となっていますが、これの回数はパスカルの三角形の数字に相当します↓
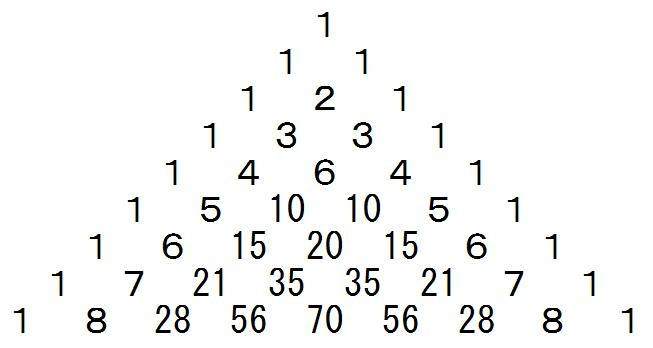
↑1を除いた箇所が、それぞれのn乗根で足される回数に相当しますね。この場合は4乗根なので、4回、6回、4回、となるわけです。
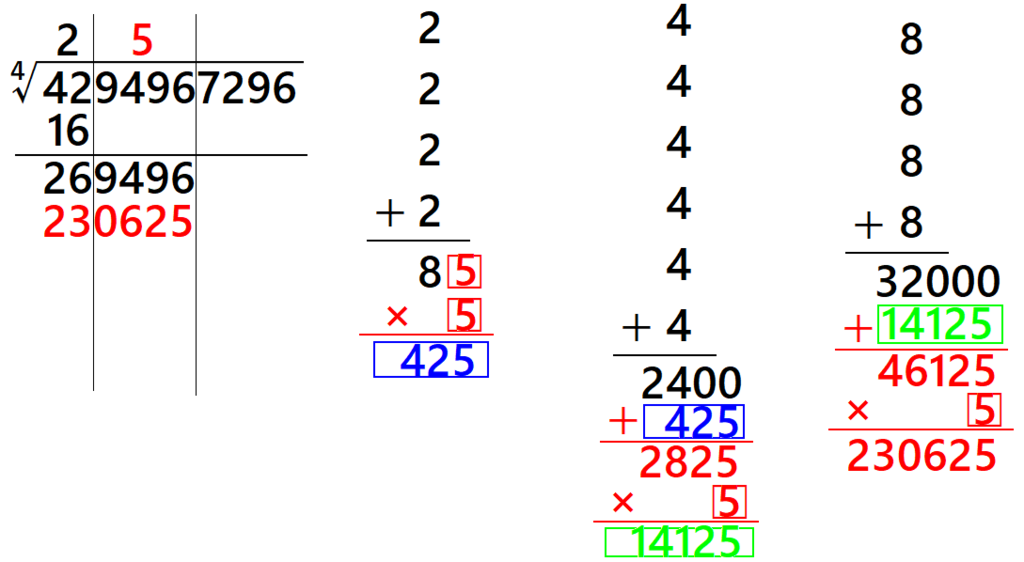
この場合は□が5なので、十の位は5になります。後は同じ要領です。

一の位は6になります。これは実際やりたくないですね……
このようにして、5乗根も6乗根も同様に筆算することができます。メリットは何でしょうね……割り算の筆算と同じように、一つ一つの桁がきちんと確定していくことや、慣れれば案外桁を当てることができるようになっていけることでしょうかね。
実際この筆算は、昔の日本で使われていた算木という計算道具による方法をもとに作っています。昔は算木を使ってn乗根や方程式を解いていたようなので、鍛えればできちゃうもんなんでしょう。たぶん……